It's a tall order for a programmer these days to avoid coming into contact with the term "monad". Having been introduced into Haskell in the early '90s, it's now more or less part of the mainstream, if its presence in Java is anything to go by. Look around and you'll find quite a few descriptions of what monads are 'like' – but this often begs the question: why not just say what they are?
The short answer, of course, is that monads are part of a branch of pure mathematics, and one that few will have studied: category theory. Usually taught at advanced undergraduate and at graduate level, it's sufficiently abstract to have once earned the moniker of "general abstract nonsense". And monads are not the first item on the menu: in Steve Awodey's "Category Theory", you won't find them mentioned before page 253. But arguably you can go some way towards grasping the notion of a monad from concepts that can be, and once routinely were, taught to teenagers: groups and homomorphisms. How so? Because a monad as such is essentially a structure very similar to a group; and because the business end of a monad is essentially a homomorphism.
Before all that, perhaps first a word on the kind of mathematics a programmer should reasonably expect to see and use: no one bats an eyelid when terms like "tuple", "set" and "vector" are part of a programming language; and of course the notion of a function is a fundamental one in computing, just as it is in mathematics. But how advanced, and how abstract? Edsger Dijkstra once remarked that "so-called higher order functions... are considered too fancy to even talk about to many mathematicians, they are functions that have functions for their argument and may return a function as a value", yet he met developers in industry who talked about them "as if they were the most normal thing in the world". Is category theory's level of abstraction the "new normal" in computing?
The Monadpest
It may be worth considering the experiences in a field whose relationship with mathematics (including abstract mathematics) has more than a few similarities with that of computing: physics. Not least because it wasn't initially considered to be a separate discipline: for one, mathematicians seem over the centuries to have spent an inordinate amount of time precisely calculating the orbit of planets – including Gauss with Ceres, and as late as Laplace with his "Celestial Mechanics". Newton exemplifies a time when mathematics and physics were more or less indistinguishable: Galileo may have said that "the laws of nature are written in the language of mathematics", but it was Newton who showed that more often than not the dialect was calculus, and that the laws were relations between derivatives. Physicists don't balk at being presented with a differential equation – it's their discipline's bread and butter. But abstract algebra can be another matter.
In fact one of the first major encounters between physics and abstract algebra didn't go smoothly. Group theory, which turned out in the 1920s to have important applications to the newly developing quantum mechanics, raised the hackles of a number of physicists, including Pauli who famously referred to the "Gruppenpest" – the plague of the groups. Over time, physicists stopped grumbling and made their peace with group theory. Will the same happen with programmers and the "Monadpest"? Maybe so. Although it must be said that monads are a more advanced concept.
If anything the relationship between computing and mathematics is a more "foundational" one. You can trace the origins of computing back to certain programmable machines – perhaps Jacquard's loom, or the work of Charles Babbage and Ada Lovelace; but in terms of theoretical underpinnings, which would apply to any such machine, it's hard to argue with the importance of two papers of 1936: Alonzo Church's "An Unsolvable Problem of Elementary Number Theory" and Alan Turing's "On Computable Numbers, With an Application to the Entscheidungsproblem". Church and Turing were both mathematical logicians, and these papers both answered the same fundamental question in logic (the "decision problem") posed by David Hilbert, one of the leading mathematicians of the nineteenth – yes nineteenth – and twentieth centuries. The notion of "computability" crucial to answering this question was at this time a strictly mathematical one, even though it was clear that there could – would – be a link to a mechanical or electronic device. Church and Turing had given very different answers, but they were shown to be equivalent (as was another given by Gödel). It's the vast generality of the questions that can be asked in computing – not least "what is computable" – that dictate the kind of mathematics that are involved. Perhaps we should not be surprised that here we are asked not to remember some obscure statistical measure on the fringes of mathematics, but to consider questions of structure and abstraction at its core, ones that are addressed by abstract algebra and category theory.
So it would seem reasonable to wade into abstract algebra – at the shallow end. Perhaps we should note in passing that with "plain old" algebra we are already at a certain level of abstraction: the use of symbols to represent numeric variables, along with addition, equality and the like took centuries to settle into its current form; and even though you can find Diophantus in ancient Greece using \(\gamma\) for the unknown, \(\Delta \gamma\) for its square and \(K \gamma\) for its cube, you won't find the now traditional notation of \(x^2\) representing a square until Descartes and Gauss. Rather Babylonian inscriptions find echoes in Cardano's 16th century instructions to add "the square of one-half the constant of the equation; and take the square root of the whole". Abstract algebra would begin to unmoor these symbols from their arithmetical roots, and in particular letters would come to represent not numbers but arbitrary mathematical objects, whatever these might be. This also took the name of "modern algebra", and is sometimes still referred to that way today – although nearly two centuries later this is a truly loose interpretation of the word "modern".
What is the shallow end of abstract algebra? The group. Something sufficiently simple that Grothendieck once spoke of its introduction, and of the invention of the symbol for zero, as "childish steps" without which mathematics had more or less stagnated "for a thousand years or two". Despite its abstraction, the fundamental simplicity and compactness of a the concept of a group once led it to be taught at secondary school. The Space Race had a role in kickstarting a period of mathematical teaching in various countries with an emphasis on relative "modernity" known as "New Math". In the US this involved teaching the basics of sets in primary school, and sometimes later moving on to abstract algebra. You can for instance find an 11th-grade textbook of the era describing "the very important structures with one operation called groups", continuing: "They appear throughout mathematics in many different guises. The study of groups as such is an instance of algebra at its purest."
Down with Euclid!
But it was in France that this kind of teaching was most systematic, and directed at the youngest audience. There the notion of a group was presented in the equivalent of the US 8th grade (4ème). The particularities of the French system – with its cutoffs for birthdates by calendar year and not school year – in fact mean that the phrase "taught to teenagers" is not entirely accurate: in the early 70s, a rigorous presentation of groups was in effect deemed suitable for twelve-year-olds. Of course whether twelve-year-olds typically agreed with this assessment is another matter... There were a few reasons for this enthusiastic, yet austere approach, the main one being the influence of Bourbaki, as a group of prominent, mainly French mathematicians came to be known. They published under this pen name for decades (amusing themselves by devising a fictitious backstory for Nicolas Bourbaki), and alongside their many tomes which attempted to present a coherent vision of the then state of mathematics, had a sizable influence on French mathematical teaching at all levels. (They are also responsible for the concept of a monad, inasmuch as Roger Godement was a member of Bourbaki when his "standard construction" appeared in 1958.) Among their founding members was Jean Dieudonné, whose onetime cry of "Down with triangles! Down with Euclid!" signaled the urge to move from teaching "fossilized geometry" to covering the more abstract mathematics that had come to the fore in the previous century.
One reason the concept of a group may have seemed a natural fit for secondary or even middle school was that its discoverer was himself a teenager – a certain Evariste Galois, whose tempestuous life, during a time of political turmoil that included a second French revolution in 1830, was cut short by a duel at the age of twenty. He was led to it by investigations into polynomial equations, a subject that had intrigued mathematicians for centuries, and one variant of which – Diophantine equations, for which only integer solutions are sought – would yet play a role in the development of notions behind computing, in the form of a "decision problem" posed by Hilbert. Hilbert who would note how Galois' work exemplified mathematical "independence": while "surely the first and oldest problems in every branch of mathematics stem from experience and are suggested by the world of external phenomena", eventually "it evolves from itself alone new and fruitful problems, and appears then itself as the real questioner. Thus arose... Galois's theory of equations... indeed almost all the nicer questions of modern arithmetic and function theory arise in this way." Specifically Galois was looking at quintic equations, i.e. polynomials of the fifth degree. There were well-known "solutions in radicals", which involved simple arithmetic operations and nth roots, for equations of lesser degree, including of course the general solution to a quadratic equation that most are familiar with. But the lack of progress in finding a similar solution for quintics had persuaded many mathematicians for a while that none existed. Then Ruffini had (almost) proved it, and Abel had proved it beyond any doubt. Galois knew all this, but he wanted to know why.
It's indeed striking that a mathematical notion so fundamental and with as many links to the physical world should have been unearthed by an "internal investigation". No apples falling from trees were involved. It wouldn't be the last in this vein either: when Eilenberg and Mac Lane started category theory, they were struck by the similarity of particular results between two very different branches of mathematics, and decided to get to the bottom of it.
Cardboard squares and rubber bands
There are many ways – finally – to present the notion of a group, with varying degrees of appeal to physical intuition. The French middle-schoolers presented with a Bourbaki-style textbook were given none at all – a perfunctory remark that powers of ten, when multiplied, yield other powers of ten, was all the "motivation" they were going to get. This was far removed from Mac Lane's approach, since in "A Survey of Modern Algebra" with Birkhoff he stresses that "the abstract concepts all arise from the analysis of concrete situations". Accordingly, the idea of symmetry that finds its expression in a group was illustrated by an appeal to "imagine a cardboard square laid on a plane" and later "a rubber band held in a straight line". On the assumption that programmers are less accustomed to arguments about cardboard squares and rubber bands, let's go with a different approach, much more common in software: the idea of a pattern. Naturally it's a key notion in mathematics as well: William Thurston once said that the closest he could come to a definition of mathematics itself was "the theory of formal patterns".
The simple laws that define a group effectively describe an algebraic pattern. One difference with programming is that there you might say that something "matches the group pattern". Mathematicians, who tend to cut to the chase, say that anything matching that pattern is a group.
Thus a group is a set \(G\) and an operation \(•\) which match a certain pattern, that of the so-called group axioms. Here we can roughly follow wikipedia. Whereas the Bourbaki-influenced school text rigorously defined intermediate concepts such as relation, we can use a shortcut familiar to programmers: \(•\) is a binary operation on \(G\), i.e. combines any two elements of \(G\) to produce a third, still in \(G\) (this takes care of the first axiom of closure).
And that's it... enough to define a fundamental structure that, as noted earlier, "appear[s] throughout mathematics in many different guises". It's a kind of self-contained world with a particularly well-behaved way of combining elements. A simple example is \((ℤ, +)\), the group of integers under addition: you can add any two integers to produce a third, addition being associative; and the "inverse" of any integer \(x\) is \(-x\), such that \(x\) added to \(-x\) yields the "identity element" zero. The key to the group's simplicity is the "structural" axiom of associativity: when combining multiple elements, this takes what programmers might think of as a tree structure and flattens it out into a simple chain: no parentheses are needed. You won't find a group "under subtraction", because subtraction isn't associative: \((7-4)-3\) is not the same as \(7-(4-3)\). Associativity is often mentioned in the same breath as commutativity, an even simpler property where operands can be exchanged: \(a•b = b•a\) that holds for any \(a\),\(b\). But groups are not necessarily commutative, and when they are, they're known as abelian (a nod to Abel).
The abstract nature of the group can be seen in the variety between simple examples. The one given above is of an infinite set of numbers \((ℤ)\) under addition, but you could also have a finite set of complex numbers (e.g. the 5th roots of unity) under multiplication, or something else entirely. In fact the most common groups are not sets of numbers combined arithmetically but sets of functions combined in the most straightforward way: composition. It's here that we can see that heralded link with symmetry, and that we get closer to both category theory and programming. And here Mac Lane and Birkhoff's cardboard square example isn't so bad after all: imagining such a square "laid on a plane with fixed axes, so that the center of the square falls on the origin of the coordinates, and one side is horizontal", the symmetry is illustrated through movements by which the square is "carried into itself": namely rotations (of 0, 90, 180 and 270 degrees) and reflections (about the horizontal, vertical and both diagonal axes). An "algebra of symmetries" follows from being able to "multiply two motions by performing them in succession", with the same net effect as one of the basic motions.
In viewing groups (and later, categories) in terms of algebraic patterns, how far removed are we from the kinds of patterns we might typically see in programming? There also the usefulness of finding patterns is widely acknowledged, both because it saves work and because it usually points to something meaningful. Could you then bypass abstract mathematics entirely and view things like monads strictly in terms of software patterns? Perhaps. But in terms of usefulness there are patterns, and then there are patterns. On a hot clear day you might want to know where in a park was likely to be shady: if you limited yourself to observing the changing shadows of trees, buildings or what have you on the ground you could certainly find patterns emerging; but the more fundamental one is elsewhere: the movement of the sun in the sky – and it's a far simpler one to boot. Groups can describe in simple terms the notion of pattern itself, in its common visual sense of stripes, polka dots, etc. The basic patterns of category theory are so widespread that they give a way to relate seemingly unconnected domains throughout mathematics. With groups and categories, you might find yourself contemplating the deep structure to be found within nature – and maybe even agree with the observation "in the end, there's nothing but symmetry". With the decorator pattern? Not so much.
Not equal, but the same
Having defined the self-contained, well-behaved structures known as groups, they become "mathematical objects" along with numbers, vectors, functions, you name it. You can now treat them as objects, and in particular look at how they relate to each other. This is where the term "homomorphism" comes in – yet almost in the same breath we should mention the very similar term "isomorphism". They have virtually the same Greek etymology ("same shape" versus "identical shape"), with an isomorphism being the "ideal" version of a homomorphism. In general the most basic relationship between simple mathematical objects such as numbers is equality – even though it can sometimes be surprisingly hard to define. The most fundamental relationship between groups is however something deeper: not that they are equal, but they are structurally the same, i.e. isomorphic. It's a fundamental concept in mathematics, and gives the lie to the often widespread impression that mathematics aims to complicate things: the aim here is to simplify, sometimes dramatically, and to show that two structures with possibly very different appearances are, for all intents and purposes, the same. If you paint a car bright yellow you'll have changed its appearance (probably), but you won't have changed anything fundamental about the car. That two groups are isomorphic tells us that the only difference is the paint job, and it's of no consequence.
For groups to be isomorphic we need to have an isomorphism between them, which is a bijection (one-to-one mapping) \(F\) between the two underlying sets with one simple property: if \((G_1, •)\) and \((G_2, *)\) are the groups, then for any \(a, b\) in \(G_1\), $$ F (a • b) = F(a) * F(b) $$ This minimalist structural axiom, recalling somewhat the associativity axiom of the group, is enough to guarantee that the structure of \((G_1, •)\) is faithfully replicated by \((G_2, *)\). For instance the identity element \(e_1\) in \(G_1\) is mapped to the identity element \(e_2\) in \(G_2\) such that \(e_2 = F (e_1)\), and from there you can easily show that \(e_2\) behaves as the identity element in \(G_2\), i.e. does nothing. As an example of an isomorphism, consider \((ℝ, +)\), i.e. the real numbers under addition, and \((ℝ^{+*}, \times)\), i.e. the strictly positive real numbers under multiplication. The first group is very similar to the integers under addition that we saw earlier. In the second group the identity element is now the real number \(1\), since \(1\) is the "do nothing" element for multiplication. In this case the exponential function is an isomorphism, since it's a bijection between \(ℝ\) and \(ℝ^{+*}\) such that \(e^{a+b} = e^a \times e^b\). Through exponentiation, a structure involving addition has morphed into an entirely equivalent one involving multiplication (which you could revert using a logarithm). In passing this example suggests some kind of fundamental symmetric relationship between sum and product, one that category theory will state very clearly and simply.
This kind of deep structural equivalence is not restricted to groups of numbers under arithmetic operations. In computing a striking illustration is the so-called Curry-Howard isomorphism, a full equivalence between seemingly vastly different areas that took decades to spot: mathematical proofs and computer programs.
With a homomorphism we're no longer in the "ideal" territory of the isomorphism, because a homomorphism is not guaranteed to be a bijection, in which case it can't be inverted. For instance, instead of just the identity element \(e_1\), several elements of \(G_1\) (the so-called "kernel") could map to the identity element \(e_2\) of \(G_2\). But crucially the same basic structural axiom holds: \(F (a • b) = F(a) * F(b)\) for any \(a, b\) in \(G_1\). This guarantees that a homomorphism broadly preserves the group's structure: you may not be able to revert from \(G_2\) to \(G_1\), but you still know that it behaves in much the same way.
A standard construction
The connection with monads? A monad provides the means for the "standard construction", as Godement originally called it, of... a homomorphism. A particular homomorphism, and one not between groups but between categories (called a functor), but which satisfies the exact same axiom. We're still looking for such a function \(F\), not necessarily invertible as is an isomorphism, but one whose fundamental characteristic is that it preserves structure. And it turns out that the monad itself, this means of constructing the end product of the homomorphism, can be viewed as something which is nearly a group: a monoid (the difference being that in a monoid elements don't necessarily have inverses, not unlike the distinction between homomorphism and isomorphism).
In computing we'll be looking at structures – not quite groups, but similar – made up of functions that are combined straightforwardly through composition. Homomorphisms between such structures can map functions to new ones in a great variety of ways, but always such that overall behavior is preserved: the new functions interact with each other in much the same fashion as the original ones. Another way of saying that a homomorphism preserves structure is that it "doesn't interfere" with the original structure. You can begin to get a sense of why in software monads are often associated with "extending" a type: one route to producing new functions with the same interactions as the old is to embed them in something larger, to add unrelated behavior in a "new dimension". If your original functions yielded integers, the ones produced by homomorphism might yield pairs of integers, with the original value "embedded" as one of the values of the pair. But there are other types of homomorphism, for example ones which instead of adding dimensions are "forgetful" of them.
Groups – or at least the related "semigroups" – even make a direct appearance in practical computing, as embodied by that decades-old poster child for efficiency, C++: Alexander Stepanov "realized that the ability to add numbers in parallel depends on the fact that addition is associative... In other words... that a parallel reduction algorithm is associated with a semigroup structure type. That is the fundamental point: algorithms are defined on algebraic structures." The result was the Standard Template Library (STL). For Bjarne Stroustrup this quest for "'the most general and most efficient code' based on a rigorous mathematical foundation" resulted in "unsurpassed flexibility and – surprisingly – performance."
A generalized group
Nearly two centuries after Galois' work, has group theory run its course, or fallen out of favor? Hardly. Where the Erlangen Program led by Felix Klein in the late nineteenth century had sought to characterize various geometries – once Euclidean geometry had been knocked off its pedestal as the one true geometry – notably in terms of transformation groups, the modern Langlands Program is an even more vast group-related undertaking: Peter Sarnak calls it "one of the great insights into twentieth-century mathematics... a beautiful synthesis of the theory of numbers and symmetry – the theory of groups – specifically Lie groups". Make that twenty-first-century mathematics as well, as confirmed by the 2018 Abel Prize awarded to Robert Langlands for his "visionary program connecting representation theory to number theory." Lie groups essentially describe continuous symmetry, of the sort given by rotations through any angle, as opposed to the discrete ones we considered earlier which simply permuted a handful of vertices. So-called representations of groups in a sense make them more concrete, by finding equivalent (isomorphic) groups that are in effect matrices under multiplication. It's the approach Weyl had used to apply group theory to quantum mechanics. And it played an important role in finally proving Fermat's Last Theorem, more than 350 years after it was conjectured, as evidenced by the title of the 1993 lecture in which Andrew Wiles announced his proof: "Modular Forms, Elliptic Curves and Galois Representations". A cursory look at the descriptions of the research by the 2018 Fields medalists again yields references to "Galois Representations" and "representation theory". If Mac Lane could muse in the 1950s that "group theory was due for a revival", it's hard to think anyone would do so today.
And category theory? As Pierre Cartier and no doubt many others have pointed out, it "didn't appear in a vacuum". Group theory was an essential part of the backdrop to its development. Eilenberg & Mac Lane's seminal 1942 paper (published in 1945), "General Theory of Natural Equivalences", may start off with an example involving vector spaces, but groups and homomorphisms are the examples mentioned within the definition of a category itself, helping the reader make a new abstract theory more "concrete". Their next paper was called "Natural Isomorphisms in Group Theory". And there's also the small matter that a category is... a generalized group.
So groups and homomorphisms are fundamental, and by no means outdated concepts, teachable at an early age, which can elicit a ring of familiarity when approaching a very abstract subject for the first time. At this point you might reasonably be tempted to ask: why aren't they systematically taught first? Now there's a question... To take an example from another area of mathematics: when Hilbert, in Mac Lane's words, "extracted the formulation of the first order predicate calculus from the pedantic morass of 'Principia Mathematica'", Russell and Whitehead's treatise on logic, he presented the results in a gradual, step-by-step style. His textbook proceeds from simple predicate logic to first-order logic (with quantifiers expressing the notions "some" and "all") and finally higher-order logic, which is the sort he thought was ultimately necessary. By contrast, explaining category theory without the stepping stone of groups feels "second-order" from the get-go.
You can't help but wonder whether this approach was originally influenced by external considerations, and then became habit. With the caveat that "most practicing mathematicians see no need for the foundations of their subject" (Lambek/Scott), it seems worth mentioning that set theory and category theory can be viewed as competing foundations for all of mathematics. Even if you don't agree with Pythagoras that "everything is mathematics", those are some bragging rights. Set theory expressed in first-order logic is the traditional choice – you can define natural numbers as nested sets of the empty set, and functions as sets of ordered pairs, pairs which in turn are defined in terms of sets... you get the picture. But there's a case to be made for functions being more appropriate building blocks than sets, and category theory a better foundation than set theory. Awodey adds type theory to the list of contenders, and while admitting that all three are "mathematically equivalent" and have their own advantages and shortcomings, generally seems to feel that category theory has a "structural approach" that is "more stable, more robust, [and] more invariant" than the others. Mac Lane had once conceded that "there is as yet no simple and adequate way of conceptually organizing all of Mathematics". On a less diplomatic day he presented a lecture with the title "Set theory is obsolete".
Non-mathematical considerations had certainly played a role in what remains a significant missed opportunity, and one which surely slowed down the general acceptance of category theory: its absence from Bourbaki's tomes. This despite Bourbaki's overriding emphasis on the idea of structure, in line with Dieudonné's observation that "since about 1840 the study of specific mathematical objects has been replaced more and more by the study of mathematical structures". Mac Lane observed that his onetime attempts to win over its members were hampered by a "command of the French language... inadequate to the task of persuasion". He does not mince his words about the result: "The official Bourbaki discussion of mathematical structure... is perhaps the ugliest piece of writing to have come from Bourbaki's pen. Nobody else makes much use of this, and Bourbaki... was too conservative to recognize other better descriptions of structure when they arose." He may also have mentioned the "cold, hard fact" that category theory was not invented in France. How did Bourbaki miss the boat on this one? While it's not inconceivable that a "made in France" label would have led to a warmer reception, Bourbaki's strongest influence was after all (arguably) that of David Hilbert. As Cartier tells it, most members were not only familiar with category theory but used it regularly, to say nothing of Eilenberg who had been a member since 1950. Grothendieck's suggestion that they rework the existing tomes to incorporate category theory seems to have foundered on the objections of a couple of members, particularly Dieudonné whose role as industrious scribe gave his opinions weight. As a consequence, adoption in France was slower than it would have been. Fast-forward a few decades though and the name OCaml derives from the "Categorical Abstract Machine". And in a move which you might suppose will be followed elsewhere, the term "group homomorphism" has been supplanted there by "group morphism", a clear nod to category theory. Whatever the historical missteps, there is no reason at all to somehow oppose groups and categories, complementary and pivotal abstractions.
That said... there's a limit to the amount of insight you're going to get about monads from the notions of group and homomorphism alone. There might after all be a case for picking up a few rudiments of category theory. What the heck.
The right generality
The one characteristic of category theory familiar to most is its high level of abstraction. Tom Leinster calls it "a bird's eye view of mathematics". It jibes with a certain view of mathematicians, who, as Feynman put it somewhat schematically in a lecture, "like to make their reasoning as general as possible. If I say to them, 'I want to talk about ordinary three dimensional space', they say 'If you have a space of n dimensions, then here are the theorems'. 'But I only want the case 3', 'Well, substitute n=3.'!" This contrasts with the physicist, who "is always interested in the special case" and "never interested in the general case." But Mac Lane would not have recognized such a characterization: for him, "good general theory does not search for the maximum generality, but for the right generality." When does added generality yield diminishing returns? He cites a technical example from Bourbaki: a clumsy universal construction that accomodated "the ideas of multilinear algebra that were important to French Mathematical traditions". We could also cite a more modern example: the mustard watch. Proposed by an alter ego of Jean-Yves Girard, this "generalisation of the concepts of watch and of mustard pot" does lead to some interesting theorems ("a mustard watch with no mustard in it is at least as precise as an ordinary one") and asks the obvious questions ("what is the point of knowing [the] time if you cannot get mustard?" – indeed), but it's not quite the right generality. Category theory is the right generality in terms of being applicable across mathematics; the problem with learning it is in being presented with that generality right away.
That a field with as wide as scope as category theory should have its roots in the coming together of separate branches of mathematics is perhaps not surprising. One of them of course was abstract algebra. Groups had now been complemented notably with rings and fields, where another operation is added – typically the two operations are now thought of as generalizing addition and multiplication. Unlike rings, fields mandate the existence of inverses for multiplication, i.e. division, except for zero – and this stipulation of such a special case, built into the very definition of a field, is often where things get interesting. You could stick to integers (\(ℤ\)) for a ring, but for a field would have to move on to something like rational (\(ℚ\)) or real (\(ℝ\)) numbers. The development of the theory of these structures was being led by Emmy Noether at Goettingen. (Hilbert had argued for her inclusion on the faculty, since he did "not see that the sex of the candidate is an argument against [it]... After all, the Senate is not a bathhouse"; and when there remained objections he arranged for lectures announced as his to be delivered by her instead.) Word of these developments reached Mac Lane via Oystein Ore, one of Noether's students who was now teaching group theory at Yale. Mac Lane then "discovered the developing ideas of modern abstract algebra", adding that "the work of Emmy Noether and her successors indicated to me that there were brand-new ideas to be found in mathematics".
Another branch of mathematics in the mix was topology. It shares with abstract algebra a certain quality of cutting to the essential – the standard joke is that a topologist can't tell a coffee mug from a donut: in this "rubber sheet geometry", sameness depends on whether you can continuously deform one shape into another, and their common basic property of "having a hole" is what remains when you do this. Of course, if such visually distinct objects are "the same" (and yes, this does entail a notion of isomorphism, a "topological isomorphism" known as a homeomorphism), then finding ones that are genuinely different can lead to some unusual shapes indeed... one of which had a direct role in the inception of category theory. What's more, with a similar focus on what actually matters – structure – and disregard for what doesn't – appearance –, abstract algebra and topology were a natural fit. As early as 1895 Poincaré had brought them together with the notion of homotopy, which would eventually allow the insights of group theory to be applied to topology. "Algebraic topology" was being developed in earnest at Princeton in the 1930s when Feynman came into contact with it: "although the mathematicians thought their topology theorems were counterintuitive, they weren't really as difficult as they looked... Paul Olum... tried to teach me mathematics. He got me up to homotopy groups, and at that point I gave up." (Feynman's invention of path integrals has been known to perplex mathematicians.) This long history hasn't prevented homotopy from illustrating yet again that there are "brand-new ideas to be found in mathematics", in the shape of homotopy type theory, proposed by Voevodsky in 2013. With it another contender for the foundations of mathematics has appeared, one with several appealing features in terms of computability, and at its heart an axiom of striking simplicity (the univalence axiom), that implies no less than that "isomorphic structures are equal". There is no paint job after all.
A coincidence that wasn't
Category theory may have been about a coming together of mathematical branches, but it was also about a meeting of mathematicians who struck up a fruitful partnership. Samuel Eilenberg shared with Saunders Mac Lane a no-nonsense personality and was known for an "insistence on getting to the bottom of things". Hyman Bass described him as "preeminently a formalist. He fit squarely into the tradition of Hilbert, Emil Artin, Emmy Noether, and Bourbaki." He continues: "Complexity and opaqueness were, for him, signs of insufficient understanding". While Mac Lane had written a dissertation on logic, in addition to studying abstract algebra and some topology, Eilenberg had become an expert in algebraic topology. It was he who brought to the attention of Mac Lane a remarkable similarity between a result Mac Lane had presented in a lecture on group extensions, and a result in topology relating to a "p-adic solenoid". Here is the description of said solenoid, as given by Mac Lane: "Inside a torus \(T_1\), wind another torus \(T_2\) p-times, then another torus \(T_3\) p-times inside \(T_2\), and so on..." The similarity of these results from separate mathematical branches was like a red rag to a bull. "The coincidence was highly mysterious. Why in the world did a group of abelian group extensions come up in homology? We stayed up all night trying to find out 'why.' Sammy wanted to get to the bottom of this coincidence."
How do you approach the basics of category theory? Perhaps you agree with Abel that the right way is in "studying the masters, not their pupils". If so Mac Lane's standard, "Categories for the Working Mathematician", certainly qualifies, however it calls on a breadth and depth of mathematical knowledge that programmers typically don't possess. The first sentence of Chapter 1 sets the tone: the category axioms will be given "without using any set theory". If this autonomous approach to establishing category theory certainly makes sense from Mac Lane's point of view, it doesn't necessarily suit ours, and that's before you consider that the initial concepts are those of "metagraph" and "metacategory". If anything you're better off reading the Eilenberg & Mac Lane's original definition in their 1942 paper "General Theory of Natural Equivalences", which is simpler and generally tries to be more helpful to the reader. It could be a sign of the times: papers of around that time and earlier – for example those of Alonzo Church – seem to try to present concepts in a way that will be more easily grasped, using non-technical language where possible. Poincaré said that to understand a theory, you had to see the reasons for which it was chosen. Could you grasp it if presented "from the outset in its definitive shape... without any trace of the fumbling steps that led up to it?" Not really, it would then be a case of learning it by heart. Mac Lane does provide motivation for the axioms he's about to present, but for the most part the theory is described in its "definitive shape". In passing (more or less), he mentions that a category is a kind of "generalized monoid" (Awodey describes it as a "generalized group", which is implied); let's use this description not as a passing remark but as a starting point.
The group that isn't
A category loosens the requirements of a group in two important ways. The first is to do away with the stipulation that every element has an inverse: as we've seen, this yields a monoid. An example of a monoid sometimes given in computing is the "free monoid" of strings under concatenation. You can concatenate strings until the cows come home, and you'll still end up with another string, but you can't concatenate a "negative string" that would take you back where you started, as you could in a group. In general, the "ideal" world of groups and isomorphisms is replaced with a (generally) non-invertible one of monoids and homomorphisms. There's a definite direction of travel in category theory: it doesn't do to ruffle feathers by trying to go the other way.
The second and more interesting change is that the binary operation is no longer guaranteed to produce a value: it becomes a partial function. In a group, any two elements can be combined to produce a third; in a category two elements might be able to be combined, but then again they might not. This corresponds to our general intuition about functions, which can only be composed under certain conditions. (The functions we've seen thus far in groups, such as rotations and permutations, are a special, simple case, and can always be combined.) A group modified in this way becomes a "groupoid", and a monoid so modified might have become, as some have pointed out, a... "monoidoid". We know it as a category instead.
Knowing that we are dealing with a group generalized in these two ways, let's have a look at the axioms for a category. A category consists of:
The first thing you notice is the unusual terminology: objects and arrows (also called morphisms). As mathematical terminology goes, "object" is as vague as you're going to get... they weren't kidding about the high level of generality. But the terms already had a certain history: for nineteenth-century logician Frege, as Heijenoort pointed out, "the ontological furniture of the universe divides into objects and functions". And Mac Lane notes elsewhere that "at Goettingen a vector was an arrow and a vector space consisted of objects (vectors)". One difference with Frege's neat divide is that here, as we'll see, arrows themselves can be viewed as objects.
No sand, just pure theory
It also soon becomes clear that the (partial) binary operation of a category, instead of being represented by various symbols as in a group, always seems to be \(∘\), in other words composition. To simplify matters further, it is often treated as optional: \(g∘f\) becomes simply \(gf\), corresponding to our usual notation for a product. The use of the terminology "domain" and "codomain" adds to the impression that what we have is a generalized group of functions. But that would be too easy.
Dana Scott summarizes it this way: "What we are probably seeking is a 'purer' view of functions: a theory of functions in themselves, not a theory of functions derived from sets. What, then, is a pure theory of functions? Answer: category theory." The reason the use of the word "function" is studiously avoided, despite including its accoutrements of domain and codomain, is that we are not looking at functions as we know them. Where tradition defined a function as a rule (e.g. \(x \rightarrow x^2\)), and later set theory defined it as set of pairs, category theory takes a minimalist, hands-off approach: a function is anything – literally anything – that behaves with other functions in the way we expect. This means above all that their composition, when permitted, is associative. (You can verify that traditional functions compose associatively: it's analagous to making a chain out of three elements, where the two joins involved can be done in either order.) The temptation when being presented with examples that are not traditional functions, such as inequalities or logical inferences, is to think "fine, but besides those outliers what we're really talking about is the usual functions between sets". It's a temptation that should be resisted, because notions such as monads rely on non-traditional functions. In summary a category is not a generalized group of functions: it's a generalized group of generalized functions.
This axiomatic definition of arrows, i.e. generalized functions, means our traditional approach to handling functions is thrown out the window. Even when we are, in fact, dealing with plain old functions between sets – and this is still the most common case in computing – we won't be concerned with what the value of the function is for any particular input, which takes some getting used to. While at Goettingen Mac Lane heard Weyl remark that set theory "contains far too much sand"; the same criticism can't be levelled at category theory. If we stop to consider arbitrary equations between functions, say \(fg = h\), we might be tempted to "solve" for \(f\) using the inverse of \(g\) (if it exists) and say \(f = hg^{-1}\). But category theory is loath to reverse the directions of arrows. When it does, it reverses them all at once, thereby producing a slew of "co"-elements – dual notions of coproduct, colimit... and the like. (This leads to category theory's version of a mathematical food joke: what does a category theorist call a coconut?)
If your view of functions is so detached that you don't consider their value for any particular input, what exactly can you say about them? As it happens, quite a lot. If you had a bee colony where for the sake of argument all bees had the same appearance, you could still work out which one was the queen bee from the interactions with others. Category theory has the makings of a mathematical whodunnit, where the clues don't seem like much but add up to something. The preface to "A Survey of Modern Algebra" held that "the most striking characteristic of modern algebra is the deduction of the theoretical properties of such formal systems as groups, rings, fields, and vector spaces." In turn Mac Lane and Eilenberg would explore that which could be deduced from the axioms of a category.
One characteristic of the arrows is that by and large they preserve structure: in the case of groups, this means homomorphisms; for vector spaces, linear transformations, etc. And what about the vanilla case of functions between sets? Well there too... in the sense that there's no structure to preserve. (These categories are respectively known as Grp, Vect and Set, illustrating the custom of naming categories according to the objects they contain. Set is of most interest in programming.) The notion of a group fits nicely into the stratified world of categories: it's simply a category with one object. (So in a sense group theory is subsumed by category theory – but in practice that wouldn't be the "right generality".)
Another readily apparent characteristic of category theory is the heavy use of diagrams, specifically "commutative diagrams". Whereas addition was "commutative" in the sense that you could "exchange" arguments (i.e. \(a+b = b+a\)), here the diagram is commutative in the sense that you can "exchange" paths of composition that lead from the same starting point to the same end point: they're guaranteed to be equal. When considering a very basic example of commutative diagram
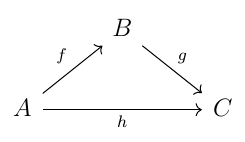
We probably shouldn't be too surprised that in a theory where the notion of a function itself is given in terms of its (collective) properties, and not what it "is", other concepts and definitions follow a similar approach. They are often characterized not by a construction but by a "universal property". The language used to do so on the whole has a relatively limited, sweeping vocabulary, making full use of "there exists" and "for all". These are familiar terms from first-order logic, where they have well-known associated symbols (\(∃\) and \(∀\), the inverted E and A due to Peano and Gentzen, respectively). Here there's a slight twist, in that existence is usually narrowed down to "there is a unique" (often written \(∃!\) in logic), specifying an arrow that typically "slots in" to a commutative diagram. Again it may seem peculiar that we are not asked to consider the value of a function for any particular input, but for some types of arrows (inequalities, logical inferences), this notion doesn't even apply. Where it does apply, notably for functions between sets, it's not that the notion has suddenly become unimportant, rather that it's typically hidden by the blanket requirement of a commutative diagram: \(gf = h\) means that for all suitable \(x\) (namely in the common domain of \(f\) and \(h\)), we have \(g(f(x)) = h(x)\). So quite a stringent requirement after all. The fact that the variable \(x\) has in effect disappeared, because of the kind of sweeping statements that are being made, is not without precedent: witness the combinatory logic of Schönfinkel and Curry. There the clashes between variable names that can occur in the lambda calculus are avoided because... there are no variables.
It may be that it's the arrows that matter, but to start off with such property-based definitions tend to concern objects instead. Given a category \(\bf C\), an initial object \(0\) has the property that for any object \(A\) in \(\bf C\), there's a unique arrow from \(0\) to \(A\). Similarly a terminal object \(1\) is such that for any object \(A\), there's a unique arrow from \(A\) to \(1\). For instance in Set, there is only one initial object (the empty set), but a host of terminal objects, i.e. every singleton (one-element) set. This may not quite fit the queen bee analogy, but there's still the idea that particular objects are characterized relatively, "structurally" by their connections to others, in this case to all others.
Products revisited
The categorical definition of a product takes the property-based approach one step further. It's what Awodey calls "probably the earliest example of category theory being used to define a fundamental mathematical notion." The most illustrative example is probably the product of sets, in other words the cartesian product:
(For finite sets this is of course closely related, through the set sizes, to the usual notion of the product of two natural numbers.) If we imagine \(A\) and \(B\) to be "axes" containing numbers, and \(A \times B\) to be all the possible pairs of "coordinates" produced in this way, we can see why the function \(π_1: A \times B \rightarrow A\) such that \(π_1 (a, b) = a\), which effectively selects the first coordinate, is referred to as a projection function (onto \(A\)) – and there is a similar function \(π_2\) that projects onto \(B\). This seemingly intrinsic property of a product – that there is always a way to recover its original component objects, through "projection" – hints at the (admittedly quite abstract) definition of a product that Mac Lane eventually settled on. This states that for a given category \(\bf C\), the product of objects \(A\) and \(B\) is an object \(A \times B\), together with projection arrows \(π_1: A \times B \rightarrow A\) and \(π_2: A \times B \rightarrow B\), that satisfy a certain universal property: for any object X in \(\bf C\), and arrows \(f: X \rightarrow A\) and \(g: X \rightarrow B\), there is a unique arrow \(u: X \rightarrow A \times B\) (indicated here and similarly elsewhere by a dashed line) that slots in to "make the diagram commute":
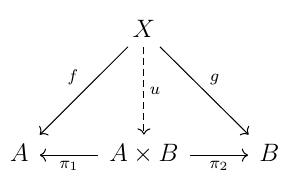
In keeping with the general approach seen so far, there is no direct construction of "the" product of two objects: we simply know that a product, if it exists, satisifies the given universal property, which more or less says that projection works as we would expect it to. It's a little bit like stating that a line through a given point is parallel to another if it doesn't intersect it. There's a difference, though, in that you can't prove that such a line is unique: this has to be stated by axiom, if indeed we're talking about Euclidean geometry. Here you can show fairly straightforwardly that products are unique "up to isomorphism" (i.e. there exists an isomorphism between any two of them), which is often as good as you're going to get in something as structural as category theory. The commutative diagram has another advantage: by simply reversing the direction of its arrows you arrive directly at the characterization of a "coproduct", also known as a "categorical sum" and accordingly denoted by "\(+\)" instead of "\(\times\)". This relationship between product and sum may recall the early example of a pair of isomorphisms that transformed a group under multiplication into one under addition, and back.
Products defined in this way are noteworthy for another reason: they are technically triples, and what's more ones with a certain "shape": a central object sandwiched between two arrows that in some sense can be seen as opposites. This arrow-object-arrow formation is in some ways a "dual" version of the object-arrow-object pattern which is fundamental to category theory. It's by no means the last time that this mathematical shape will crop up: among many others it characterizes a certain construction known by the name "triple" until Mac Lane decided to call it a monad.
While products are often discussed early on in category theory, they weren't proposed by Mac Lane until 1950, nearly a decade after the initial paper which presented what he and Eilenberg were actually interested in: natural transformations. As the story goes, the notion of a category itself arose to define a functor, which in turn was necessary to define a natural transformation. It's worth considering here why this struck them as a particularly important concept.
Transformations without artifice
Those mathematicians who wish to "get to the bottom of things" tend to give short shrift to what they view as distractions along the way. One example is combinatory logic: Schönfinkel argues that "a variable in a proposition of logic is, after all, nothing but a token that characterizes certain argument places and operators as belonging together; thus it has the status of a mere auxiliary notion that is really inappropriate to the constant, "eternal" essence of the propositions of logic." In the same vein Mac Lane states that "a vector is geometrical; it is an element of a vector space, defined by suitable axioms... [it] is not an n-tuple of numbers until a coordinate system has been chosen. Any teacher and any text book which starts with the idea that vectors are n-tuples is committing a crime for which the proper punishment is ridicule. The n-tuple idea is not 'easier,' it is harder; it is not clearer, it is more misleading." This meant that there was something unsatisfying to Mac Lane about transformations of vector spaces that depended on the "auxiliary notion" of coordinates. In their seminal 1942 paper "General Theory of Natural Equivalences", he and Eilenberg begin by examining the isomorphisms between a vector space – i.e. a collection of "objects (vectors) which could be suitably added and multiplied by scalars" – and its dual. (Duality brings us to another deep structural notion in mathematics, one that Michael Atiyah defines as a principle that "gives two different points of view of looking at the same object". For instance in planar geometry, the role of points and lines in a theorem can sometimes remarkably be interchanged to yield a "dual theorem" describing a visually very different construction, but on some level with the same abstract structure.) Given a vector space \(L\), the dual space \(T(L)\) consisted of "all real valued linear functions t on \(L\)" – such as dot products – which themselves could be manipulated as vectors. \(L\) and \(T(L)\) were isomorphic, but the problem was the following: "such an isomorphism cannot be exhibited until one chooses a definite set of basis vectors for \(L\), and furthermore the isomorphism which results will differ for different choices of this basis."
It wasn't until you took the process one step further that the smoke cleared: for the dual of the dual, or bidual, \(T(T(L))\), "one can exhibit an isomorphism between \(L\) and \(T(T(L))\) without using any special basis in \(L\). This exhibition of the isomorphism \(L \equiv T(T(L))\) is 'natural' in that it is given simultaneously for all finite-dimensional vector spaces \(L\)." They were arriving at a precise definition of the term "natural", which as Emily Riehl notes, "had been used colloquially by mathematicians to mean 'defined without arbitrary choices'". There was, after all, a way to do without the artifice of coordinates to get at the heart of the matter.
The definition of a natural transformation is not that much more complex than that of a product, but it's a step up in terms of abstraction, as it involves arrows between categories. This is, to a point, something we've seen before: a group homomorphism transforms one group (a particular kind of category) into another. As alluded to earlier, the arrows from one category to another – naturally, structure-preserving – are known as functors: Awodey describes a functor early on as a "'homomorphism of categories'". A functor \(F\) between categories \(\bf C\) and \(\bf D\) maps arrows in a way that satisfies the same structural axiom we saw for groups (with the slight simplification in notation that the operator in both \(\bf C\) and \(\bf D\) is assumed to be composition, and written ∘ in both cases, even though it could technically differ between \(\bf C\) and \(\bf D\)): $$ F (g ∘ f) = F(g) ∘ F(f) $$ (It also preserves the identity element (\(F(1_A) = 1_{FA})\), but this can be shown for group homomorphisms as well.) Although this mapping of arrows is the essence of the functor, and corresponds to the mapping of set elements in a group homomorphism, a functor is also considered to map the arrow's sidekick objects: \(F (f: A \rightarrow B) = F(f) : F(A) \rightarrow F(B)\), and so "preserves domains and codomains". So far, there is little to differentiate this "homomorphism of categories" from a group homomorphism. But a natural transformation will introduce a crucial distinction in the way it is used, in so doing blurring the lines between levels of abstraction. In our first example of an isomorphism, the group \((ℝ, +)\) was transformed into \((ℝ^{+*}, \times)\) by the exponential function \(F(x) = e^x\). There \(F\) appeared clearly as something "external", and served only to convert one group of numbers into another. By contrast some of the power of category theory can be seen in the way, via natural transformations, it brazenly mixes functors between categories and arrows within categories: they are all, in the end, (generalized) functions.
What, then, is a natural transformation? A "morphism of functors". If you're reflexively thinking of a set of functor pairs, this isn't "the right generality". The domain of a natural transformation is not a set, not even a singleton: it's simply a functor. The arrow we're describing is a transformation from that single functor to another. But let's consider first somewhat more familiar territory, the idea of mapping one function to another, as is known in computing by "higher-order function". What general form might this mapping take, not in terms of somehow simply listing pairs of functions as input and output but in providing the more traditional notion of a "rule"? An example would be the "differential operator" which takes a function and returns its derivative, often according to a simple algebraic recipe. But in the general spirit of category theory, let's stick to a construction that uses its central tool: composition. If you wanted to convert a function \(f:A \rightarrow B\) to a function \(g:A' \rightarrow B'\) in this way, you would presumably define the transformation \(F\) along the lines of $$ g = F(f) = h'∘f∘h $$ for some functions \(h\) and \(h'\) ("h prime"). You know something else for free: the "plumbing" has to work out. To convert the domain (\(A\)) and codomain (\(B\)) of the original function, \(h\) and \(h'\) have to act in some sense as "adapters", with \(h:A' \rightarrow A\) and \(h':B \rightarrow B'\), yielding a chain \(A' \rightarrow A \rightarrow B \rightarrow B'\) that results in the desired \(g:A' \rightarrow B'\).
Let's now have a look at the definition of a natural transformation. Given categories \(\bf C\) and \(\bf D\), and functors \(F\) and \(G\) between those categories, a natural transformation i from \(F\) to \(G\) is a family of arrows \(η_A\) contained in \(\bf D\), but indexed by objects in \(\bf C\). Thus to each \(\bf C\)-object A corresponds one of these component \(\bf D\)-arrows \(η_A:F(A) \rightarrow G(A)\), with the following property: for any \(\bf C\)-arrow \(f:A \rightarrow B\), the following diagram commutes:
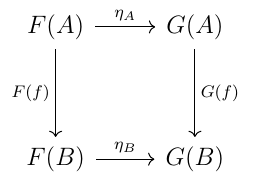
As with the earlier definition of a product, this doesn't "construct" a natural transformation, but states the property it (or more precisely all of its components) must satisfy if it exists. The definition as given illustrates something noteworthy about a natural transformation: it's not a function in the traditional sense. The clue was in the name, after all. It's a collection of functions that, taken together, behave as arrows are expected to behave, above all by composing associatively with other similar, matching arrows. As it happens a natural transformation makes mathematically precise the notion of a generic function in computing. If you've ever wondered whether a generic function, with its type undefined, is really a function: in the set-theoretic sense it isn't, but in terms of category theory it is.
What though is that particular commutative diagram actually saying? How exactly is it transforming \(F\) into \(G\)? To get an idea of what it's saying, we may want to look at what it's almost saying. What the diagram gives us is the arrow equation \(G(f)∘η_A = η_B∘F(f)\). What it says with a little artistic license is that \(G(f) = η_B∘F(f)∘{η_A}^{-1}\), which is essentially the mapping of \(F(f)\) to \(G(f)\), for a given \(f\), that we are looking for, one that fits the general expected shape of transformation through composition. It would in fact say exactly that if we knew that \(η_A\) had an inverse, but we don't. So category theory does the next best thing, which is to pin down the meaning of \(G(f)\) without taking that final step of defining it explicitly. It's not altogether unlike having an equation between real numbers \(ax = bc\) and refraining from expressing \(x\) as \(bc/a\), if you don't know whether a has an inverse (i.e. isn't zero). The stolid two-and-two, rectangular symmetry of the commutative diagram can in fact nearly be seen as one-and-three, and with it another product-like definition in terms of a "triple with opposites".
The component arrows of the natural transformation cut across the general direction of travel of arrows within \(\bf D\), as they join their respective start and end objects (domain and codomain). They are in some sense "adapters" that adjust the various \(F\)-mapped arrows to \(G\)-mapped ones solely on the basis of their differing endpoints. There is a graphical interpretation: Awodey likens the functors from categories \(\bf C\) to \(\bf D\) to "pictures" of \(\bf C\) in \(\bf D\), and a natural transformation to a "cylinder" with a picture at each end.
Let's consider a little more closely the general mathematical shape of a triple whose outer elements are in some sense opposites. Of the many examples which fit this description, there's for instance the notion of conjugacy: elements \(a\) and \(b\) of a group \(G\) are conjugates if there is an element \(g\) in \(G\) such that \(b\) = \(gag^{-1}\). Translated to linear algebra this becomes matrix similarity: square matrices \(A\) and \(B\) are similar if there's a matrix \(P\) such that \(B = P^{-1}AP\). If matrix multiplication were commutative, we could switch the order of the operands and the outer elements would simply cancel each other out. But it isn't, suggesting that a direction of travel in such triples yields not equality but an approximation thereof. There's a hint of the shape in first order logic, where the universal (\(∀\)) and existensial (\(∃\)) quantifiers can be expressed in terms of one another, in an extension of De Morgan's laws: if \(P(x)\) is a predicate, then \(∀xP(x)\) is equivalent to \(¬(∃x¬P(x))\). E.H. Moore, who had influenced Mac Lane while at Chicago (persuading him to study at Goettingen), once said that "the existence of analogies between central features of various theories implies the existence of a general abstract theory which underlies the particular theories and unifies them with respect to those central features." The general abstract theory in question turned out to be category theory; and the part of that theory which best explains these similar mathematical shapes is that of adjoint functors.
Adjointness everywhere
With adjoints we are very close to the notion of a monad: they weren't discovered, by Daniel Kan, until 1956, published in 1958, and Godement followed up with his "standard construction" the same year. Awodey makes "the admittedly provocative claim that adjointness is a concept of fundamental logical and mathematical importance that is not captured elsewhere in mathematics". According to Mac Lane, "the slogan is 'Adjoint functors arise everywhere'". In fact we've already seen a major example: the age-old logical quantifiers of "for all" and "there exists" were shown by William Lawvere to be, quite simply, adjoint functors.
Natural transformations may have shown the power of mixing homomorphisms with "ordinary" arrows, but these homomorphisms (functors) were in the same direction. Adjoint functors take us one step further by using functors in opposite directions, binding two categories together as tightly as they can be bound, even if they are quite different in nature, particularly where one has more structure than the other. It's the mathematical version not of a one-way ticket, but of a "round trip". Even if you start and end in the same category, transiting through another leaves an unmistakable "trace".
We begin again with categories \(\bf C\) and \(\bf D\), and two functors between them – except this time we'll call them \(F\) and \(U\), for reasons we'll see shortly. With natural transformations the direction of travel was from \(\bf C\) to \(\bf D\): both functors pointed this way, and \(\bf C\)-objects indexed \(\bf D\)-arrows. The commutative diagram that effectively transformed one functor into the other was then wholly within \(\bf D\). In the case of adjoints though everything is intertwined. \(F\) is still from \(\bf C\) to \(\bf D\), but \(U\) is in the opposite direction, from \(\bf D\) to \(\bf C\).
Instead of starting with a single object in \(\bf C\), an adjunction asks us to simultaneously consider arbitrary objects \(C\) and D in \(\bf C\) and in \(\bf D\). Two further objects suggest themselves: the images of these objects by the relevant functor, i.e. \(F(C)\) and \(U(D)\) in \(\bf D\) and \(\bf C\), respectively. We now have two pairs of objects that can serve as the endpoints of \(\bf C\)-arrows and \(\bf D\)-arrows: the question is, what is the relationship between such arrows? We'll consider two separate approaches and definitions.
In the first, we'll use a construction based on a universal property. If we take an arbitrary \(\bf C\)-arrow between \(C\) and \(U(D)\), can it be transformed to a \(\bf D\)-arrow between \(F(C)\) and D? In fact we'll start the other way around, with a \(\bf D\)-arrow \(g:F(C) \rightarrow D\). The obvious candidate of functor \(U\) will take it to a \(\bf C\)-arrow \(U(g)\) between \(U(F(C))\) (or more simply \(UFC\)) and \(U(D)\). But this won't be of the form we're looking for, i.e. \(f:C \rightarrow U(D)\), since the domains don't match. At the very least we require a domain adjustment – and this is where the "adapters" within natural transformations come into play once more.
So we introduce a natural transformation \(η: 1_C \rightarrow U∘F\) between "endofunctors", i.e. functors that start and finish in the same category (\(\bf C\)), where here one is the identity "do nothing" \(1_C\) and the other is a round trip from \(\bf C\) to \(\bf D\) and back again. Then an adjunction consisting of the triple \(F\), \(U\), and \(η\) satisfies the following property: for any \(\bf C\)-object \(C\), \(\bf D\)-object D and \(\bf C\)-arrow \(f:C \rightarrow U(D)\), there's a unique \(\bf D\)-arrow \(g:F(C) \rightarrow D\) such that \(f = U(g)∘η_C\), i.e. such that the following triangle commutes:
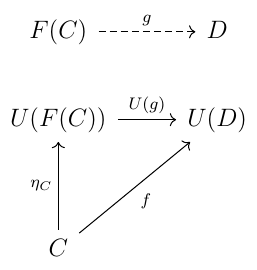
Categories \(\bf C\) and \(\bf D\) don't play symmetric roles, and accordingly there's a notion of left and right for the functors between them: \(F\) is the left adjoint to \(U\), and \(U\) is the right adjoint to \(F\), written \(F⊣U\). While \(F\) and \(U\) may go in opposite directions, they are not "true opposites". If they were exact inverses \(U∘F\) would be the identity functor \(1_C\). Instead \(1_C\) and \(U∘F\) are related by natural transformation \(η\), known as the unit of the adjunction, with its universal property given above. (Reverse all the arrows and you get the counit \(ε: F∘U \rightarrow 1_D\). If you're rusty on your Greek letters, \(η\) – "eta" – is roughly equivalent to "i", as is iota, and could be taken as emphasizing that unit is "like" identity.)
The second definition of adjoints uses the notion of "hom-set", which although derived from "homomorphism" means simply the set of arrows between two objects X and Y in a category \(\bf C\), written either \(Hom(X,Y)\) or \({\bf C}(X,Y)\). It states that an adjunction is characterized by an isomorphism \(φ: {\bf D}(F(C),D) \equiv {\bf C}(C, U(D))\) that is natural in \(C\) and \(D\) – we can just take this to mean that it's a bijection "defined without arbitrary choices". \(φ\) is in fact defined, for any \(C\) in \(\bf C\), \(D\) in \(\bf D\) and \(g: FC \rightarrow D\), by \(φ(g) = U(g)∘η_C\). (This also means, taking the particular case of \(D\) set to \(F(C)\) and \(g\) set to \(1_{FC}\), that \(η_C = φ(1_{FC})\), since \(U\) preserves identity arrows). There is thus a one-to-one correspondence between these particular \(\bf C\)-arrows (from \(C\) to \(U(D)\)) and \(\bf D\)-arrows (from \(F(C)\) to \(D\)). This definition may appear as more symmetric than the first, but they're equivalent, and there's still the same notion of left and right. The bijection can be written $$ \frac{F(C) \rightarrow D}{C \rightarrow U(D)} $$ and can also be presented as a commutative diagram:
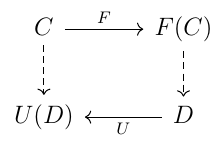
This may recall the rectangular commutative diagram of a natural transformation, but instead of being wholly contained within \(\bf D\), it spans both categories, starting with \(C\) in \(\bf C\) and \(D\) in \(\bf D\). And there is no need to squint to see a triple with "opposites" (or more precisely adjoints): the commutable paths of the rectangle are not two-and-two but one-and-three, i.e. if we name \(f\) the \(\bf C\)-arrow from \(C\) to \(U(D)\) and \(g\) the \(\bf D\)-arrow from \(F(C)\) to \(D\), then \(f = U ∘ g ∘ F\).
Such an intertwining of categories produces powerful results; it's a kind of best attempt at symmetry in a situation which is inherently asymmetric. Typically category \(\bf D\) has more structure than category \(\bf C\), and \(U\) is often a "forgetful functor", which commonly "forgets" the structure of a group, ring, field etc by mapping it to its underlying set (accordingly it's often denoted as \(U\)). In the other direction, \(F\) often constructs "free" objects with structure, such as the free monoid of strings seen earlier, by using the elements of a set as generators, in the manner of a basis for a vector space. As an example we can take Set and Grp as the two categories \(\bf C\) and \(\bf D\) (of sets and groups), with the forgetful functor \(U: {\bf Grp} \rightarrow {\bf Set}\) mapping each group to its underlying set, and conversely the functor \(F: {\bf Set} \rightarrow {\bf Grp}\) constructing the free group \(F(X)\) from a set \(X\). The underlying set of this free group, \(S = UF(X)\), is the image of set \(X\) under the "round trip" \(U∘F\): it's such that the unit \(η: X \rightarrow S\) maps each element of \(X\) to itself in \(S\). David Spivak has an evocative image for a very similar example (he replaces Grp with Mon, the category of monoids). For him adjoint functors are like "dictionaries that translate back and forth between different categories" that are not necessarily "on the same conceptual level". He asks us to consider different levels of language, contrasting baby talk made up largely of repeated sounds with adult conversations where sounds are interpreted as words and sentences. Translating the baby talk of Set involves attempting to assign a meaning to it as words in the more structured Mon, but in the other direction the translation yields merely sounds for which the meaning has been "forgotten".
Monads, or higher structure by stealth
The striking thing about monads, having looked at natural transformations and adjunctions, which both relate a pair of functors between a pair of categories, is that we're back down to a single category (\(\bf C\)). We're even back down to a single functor (\(T\)), necessarily an endofunctor from \(\bf C\) to \(\bf C\). What we have besides this is a way of relating \(T\) with iterations of itself, through two natural transformations that are the opposing bookends of our triple, and a couple of simple equalities that must be satisfied. And yet this is enough to imply the existence of a more structured category \(\bf D\), and an adjunction that binds it to \(\bf C\). In this way "every monad arises from an adjunction". You might say it's a bit like an infant mouthing an approximation to "homotopy type theory" being a giveaway that there's a world where those sounds correspond to words and concepts that make sense. So one way to view monads is as an adjunction with a hidden, more advanced category: higher structure by stealth. It also means that attempting to reduce monads in programming terms strictly to ordinary functions between sets strains credulity: their defining characteristic is the "trace" of that structure.
While it's straightforward to give the definition of a monad, the terms used and overall structure make greater sense if we consider once more those basic structures: groups and monoids.
Groups and monoids are such fundamental patterns that they begin to crop up within categories. This is particularly the case for monoids, which correspond more to the idea of a general direction of travel, where the existence of inverses can't be guaranteed. Whenever you have a means of combining two mathematical objects to produce a third of the same nature, the question can be asked: is the process associative, i.e. can such objects essentially be chained together? If all relevant objects can be combined in this way (and one of them is the "do nothing" identity object), a monoid it is. And in a category the opportunities for combination abound – beyond the composition of arrows that is its essence – particularly where you have the notion of a product of objects. The cartesian product is a near miss when it comes to forming the backbone of a monoid, since it's only associative up to isomorphism (the product set \(A \times (B \times C)\) contains elements of the form \((a,(b,c))\) as opposed to \(((a,b),c)\) in \((A \times B) \times C)\). It does nonetheless qualify as an instance of a generalized product \(⊗\), which differs from the product defined earlier, and characterizes so-called "monoidal categories" in which monoids are common. Set is one such category.
You might think that the original, minimalist definition of a monoid hardly needed reviewing; and that its depiction as "a category with one object" was the final word on the matter. But just as there is a categorical view of a product, there is a more abstract view of a monoid itself. Where the product was predicated on the existence of projection arrows, the categorical approach to defining a monoid is one where having chosen a suitable notion of object product, a binary operator on an object M is an arrow from its "square" to itself. This arrow \(μ: M \times M \rightarrow M\) ("mu") is thought of as defining "multiplication" on \(M\). The monoid \((M, μ, η)\) is completed by a second arrow \(η : 1 \rightarrow M\), where \(1\) is as before a terminal object. The associativity and identity equalities are then represented by the following commutative diagrams:
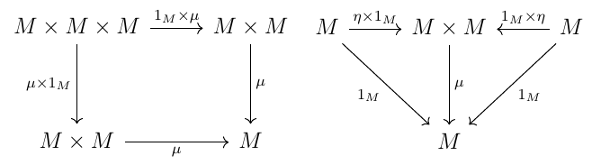
In Set, this is essentially the original definition via \((M, *, e)\), with the cosmetic difference that element \(e\) of set \(M\) has become a morphism \(η\) which picks one of the members of \(M\), an entirely equivalent construct of the identity as a "generalized element".
It's with this in mind that we can give the definition of a monad on a category \(\bf C\): it's a triple comprised of
• an endofunctor \(T: {\bf C} \rightarrow {\bf C} \)
• a unit natural transformation \(η: 1_C \rightarrow T\)
• a multiplication natural transformation \(μ: T^2 \rightarrow T\)
such that the following diagrams commute:
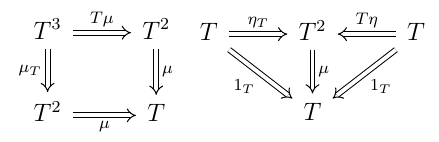
A monad (\(T, η, μ)\) thus has an unmistakable overall structural similarity with the categorical definition of a monoid, with natural transformations η (the unit) playing the role of identity and μ acting as multiplication. When viewed from a different angle, i.e. as a structure within the category of endofunctors on \(\bf C\), with multiplication represented by function composition, it is a monoid. But it's more useful to stick with the original point of view.
Note also that the idea of a binary operator on a set \(M^2 \rightarrow M\) has been generalized to \(μ: T^2 \rightarrow T\) where \(T\) is an endofunctor and \(T^2\) is its repeated application, instead of the cartesian product of a set by itself.
A typical example in computing is the list monad, or free monoid monad (on \(\bf Set\), and implying higher-structure category \(\bf Mon\)). Here the endofunctor \(T: {\bf Set} \rightarrow {\bf Set} \) maps a set \(S\) to the set of finite lists of elements of \(S\). The unit (natural transformation) \(\eta\) has components \(\eta_S: S \rightarrow TS \) mapping each element of \(S\) to the corresponding singleton list. The multiplication \(\mu\) has components \(\mu_S: T^2 S \rightarrow T S \) that are concatenation functions, flattening a list of lists into a single one.
Let's briefly review where the associativity and unit laws come from. We start by deriving the "triangle identities" for a given adjunction \(F : \bf C \leftrightarrows \bf D\) : \(U\) with unit \(η: 1_C \rightarrow UF\) and counit \(ε: FU \rightarrow 1_D\). As before for any \(C\) ∈ \(\bf C\), D ∈ \(\bf D\) and \(g:FC \rightarrow D\) we have \(φ(g) = U(g) ∘ η_C\) (the equivalent for the counit is that for any \(f:C \rightarrow UD\), \(φ^{-1}(f) = ε_D.F(f))\). And as before we use the particular case of interdependent values of \(C\) and \(D\) to derive new equalities: just as setting \(D\) to \(F(C)\) and \(g\) to \(1_{FC}\) yields \(η_C = φ(1_{FC})\), setting \(C\) to \(U(D)\) and \(f\) to \(1_{UD}\) yields \(ε_D = φ^{-1}(1_{UD})\). We can then see that \(1_{FC} = φ^{-1}(η_C) = ε_{FC}∘F(η_C)\) and \(1_{UD} = φ(ε_D) = U(ε_D) ∘ η_{UD}\), or more concisely: $$ Uε ∘ η_U = 1_U $$ $$ ε_F ∘ Fη = 1_F\ $$ A word on notation: there are no parentheses provided for when these equations are "completed" by objects: for instance \(η_U\) will become the indexed function \(η_{U(D)}\), while \(Fη\) becomes \(F(η_C)\). But somewhat similarly to Haskell where the right-associativity of type arrows and function composition means parentheses can be omitted, they can be here too. We now have a third definition of an adjunction: in terms of a unit η and counit ε that satisfy these triangle identities.
It's this simpler "equational" definition of an adjunction which yields the monad's associativity and unit laws. We start by considering a category \(\bf C\) and an arbitrary functor \(T\) from \(\bf C\) to \(\bf C\), i.e. an endofunctor. We then suppose that \(T\) is in fact the product of adjunct functors \(F\) and \(U\) to and from another category \(\bf D\): \(T = U∘F\). Since \(F⊣U\) there's a unit natural transformation \(η: 1_C \rightarrow U∘F\), so in this case \(η: 1 \rightarrow T\). There's also a counit \(ε: F∘U \rightarrow 1_D\). Among this family of indexed \(\bf D\)-arrows, there is, corresponding to the particular value of \(D\) given by \(F(C)\), a function \(ε_{FC}: F(U(F(C))) \rightarrow F(C)\), or more simply \(ε_{FC}: FUFC \rightarrow FC\). This particular \(\bf D\)-arrow can be once more sent to a \(\bf C\)-arrow by functor \(U\), yielding overall \(Uε_{FC}: UFUFC \rightarrow UFC\). This provides a function in terms of "round trips", \(μ: T^2 \rightarrow T\) (that is, \(μ = Uε_F\)). It turns out that, with a little prodding, the triangle equalities yield expressions in terms of round trips as well. Again setting \(D\) to the particular value \(FC, Uε∘η_U = 1_U\) yields \(Uε_{FC}∘η_{UFC} = 1_{UFC}\), or \(μ∘η_T = 1_T\). Composing by functor \(U\) for a given object \(C\), \(ε_F∘Fη = 1_F\) yields \(Uε_{FC} ∘ UFη_C = U1_{FC} = 1_{UFC}\), or \(μ∘Tη = 1_T\). Associativity requires a little more work, but the commutative diagram for a natural transformation from \(F ∘ U\) to \(1_D\) means that for any \(\bf D\)-arrow \(f\) between \(A\) and \(B\), in \(\bf C\) we have \(f∘ε_A\) = \(ε_B∘FUf\). Taking the particular arrow \(f = ε_B\) between \(FUB\) and \(B\), setting \(B\) to \(FC\) (i.e. \(A = FUFC\) and \(f = ε_{FC})\), and finally applying \(U\)... we arrive at \(Uε_{FC} ∘ Uε_{FUFC} = Uε_{FC} ∘ UFU ε_{FC}\), in other words \(μ∘μ_T = μ∘Tμ\). This gives us the monoid-like commutative diagrams for associativity and unit.
There's a straightforward relationship between an adjunction and the "hidden adjunction" that is a monad. Any adjunction \((F, U, η, ε)\) yields a monad \((T, η, μ)\) with \(T = UF\), \(η\) unchanged, and \(μ = Uε_F\). Conversely "every monad arises from an adjunction": given any monad \((T, η, μ)\) on a category \(\bf C\), there necessarily exists a category \(\bf D\) such that there is an adjunction (\(F, U, η, ε)\) between \(\bf C\) and \(\bf D\), again with \(T = UF\), \(η\) unchanged, and \(μ = Uε_F\). So the unit stays the same, and multiplication is a kind of conjugate of the counit, in fact known as a "whiskered" counit.
Since, then, a monad is basically equivalent to an adjunction – which after all is perhaps the pivotal notion of category theory, and appears throughout mathematics – while presenting a simpler appearance (one category, one functor), we can't be too surprised by its usefulness and increased uptake in computing. Eugenio Moggi started things off with "Notions of computation and monads" in 1991, which argued for a "categorical semantics of computation". Philip Wadler's "The essence of functional programming", describing the use of monads to "structure functional programs", announced their introduction in Haskell the following year. There is, though... the name. Mac Lane may not have done its adoption within computing any favors by overruling Godement's earlier description as a "standard construction", and Eilenberg and Moore's use of the term "triple" (which he thought had "achieved a maximum of needless confusion"). To be sure, the intention was there right from the start: he notes that "the discovery of ideas as general as these is chiefly the willingness to make a brash or speculative abstraction, in this case supported by the pleasure of purloining words from the philosophers: 'Category' from Aristotle and Kant, 'Functor' from Carnap (Logische Syntax der Sprache), and 'natural transformation' from then current informal parlance." Mac Lane's study of the philosophy of mathematics while at Goettingen may have played a role, along with the fact, in this particular case, that he had written for the philosophy journal "The Monist". You might not think the name of a mathematical concept is of much importance. But Pierre Cartier once admitted that "for a long time I didn't like groupoids because they have an ugly name... 'monoid' isn't much better", before musing about "asteroid" and "humanoid" but thankfully not moving on to the term "monad". If a prominent member of Bourbaki can be put off by a mathematical term, he can't be the only one. Dana Scott, while describing category theory as "unavoidable", also drew attention to its "odd terminology". Perhaps because of this, some programming languages use monads while heeding the maxim "don't mention the m-word". On balance, though, it would seem to make more sense to use existing terms and explain them clearly. Of course Mac Lane had an opinion about such things: best not to exhibit "carelessness... and inattention to established terminology, traits which", ahem, "we do not need to copy from the physics community."
There's a near-consensus these days that the "New Math" reformers went too far. It's hard to disagree entirely when physics teachers were obliged to teach their own, "practical" version of mathematics that had suddenly been jettisoned to make room for abstract algebra. But you might also say that the counter-reformers threw the baby out with the bathwater. Something doesn't add up about the continued unwillingness, half a century on, to teach the basic concept of a group to teenagers – a concept most associated with another teenager whose life was anything but boring. For a short while they could be made aware that there might be something more to mathematics than triangles and numerical recipes. And who knows, years later they might not be particularly fazed by the mathematical notion of a monad.
© 2018References
